Kamykowski model for fitting thermal performance curves

Usage

kamykowski_1985(temp, tmin, tmax, a, b, c)

Arguments

temp: temperature in degrees centigrade
tmin: low temperature (ºC) at which rates become negative
tmax: high temperature (ºC) at which rates become negative
a: parameter with no biological meaning
b: parameter with no biological meaning
c: parameter with no biological meaning

Value

a numeric vector of rate values based on the temperatures and parameter values provided to the function

Details

Equation: $$rate= a \cdot \big( 1 - exp^{-b\cdot \big(temp-t_{min}\big)}\big) \cdot \big( 1-exp^{-c \cdot \big(t_{max}-temp\big)}\big)$$

Start values in get_start_vals are derived from the data or sensible values from the literature.

Limits in get_lower_lims and get_upper_lims are derived from the data or based extreme values that are unlikely to occur in ecological settings.

Note

Generally we found this model easy to fit.

References

Kamykowski, Daniel. A survey of protozoan laboratory temperature studies applied to marine dinoflagellate behaviour from a field perspective. Contributions in Marine Science. (1985).

Examples

# load in ggplot
library(ggplot2)

# subset for the first TPC curve
data('chlorella_tpc')
d <- subset(chlorella_tpc, curve_id == 1)

# get start values and fit model
start_vals <- get_start_vals(d$temp, d$rate, model_name = 'kamykowski_1985')
# fit model
mod <- nls.multstart::nls_multstart(rate~kamykowski_1985(temp = temp, tmin, tmax, a, b, c),
data = d,
iter = c(3,3,3,3,3),
start_lower = start_vals - 10,
start_upper = start_vals + 10,
lower = get_lower_lims(d$temp, d$rate, model_name = 'kamykowski_1985'),
upper = get_upper_lims(d$temp, d$rate, model_name = 'kamykowski_1985'),
supp_errors = 'Y',
convergence_count = FALSE)

# look at model fit
summary(mod)
#> 
#> Formula: rate ~ kamykowski_1985(temp = temp, tmin, tmax, a, b, c)
#> 
#> Parameters:
#>       Estimate Std. Error t value Pr(>|t|)    
#> tmin 1.634e+01  3.691e+00   4.428  0.00305 ** 
#> tmax 4.881e+01  1.019e+00  47.895 4.53e-10 ***
#> a    1.000e+02  2.668e+04   0.004  0.99711    
#> b    8.469e-04  2.266e-01   0.004  0.99712    
#> c    1.214e-01  4.227e-01   0.287  0.78231    
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error: 0.3717 on 7 degrees of freedom
#> 
#> Number of iterations to convergence: 83 
#> Achieved convergence tolerance: 1.49e-08
#> 

# get predictions
preds <- data.frame(temp = seq(min(d$temp), max(d$temp), length.out = 100))
preds <- broom::augment(mod, newdata = preds)

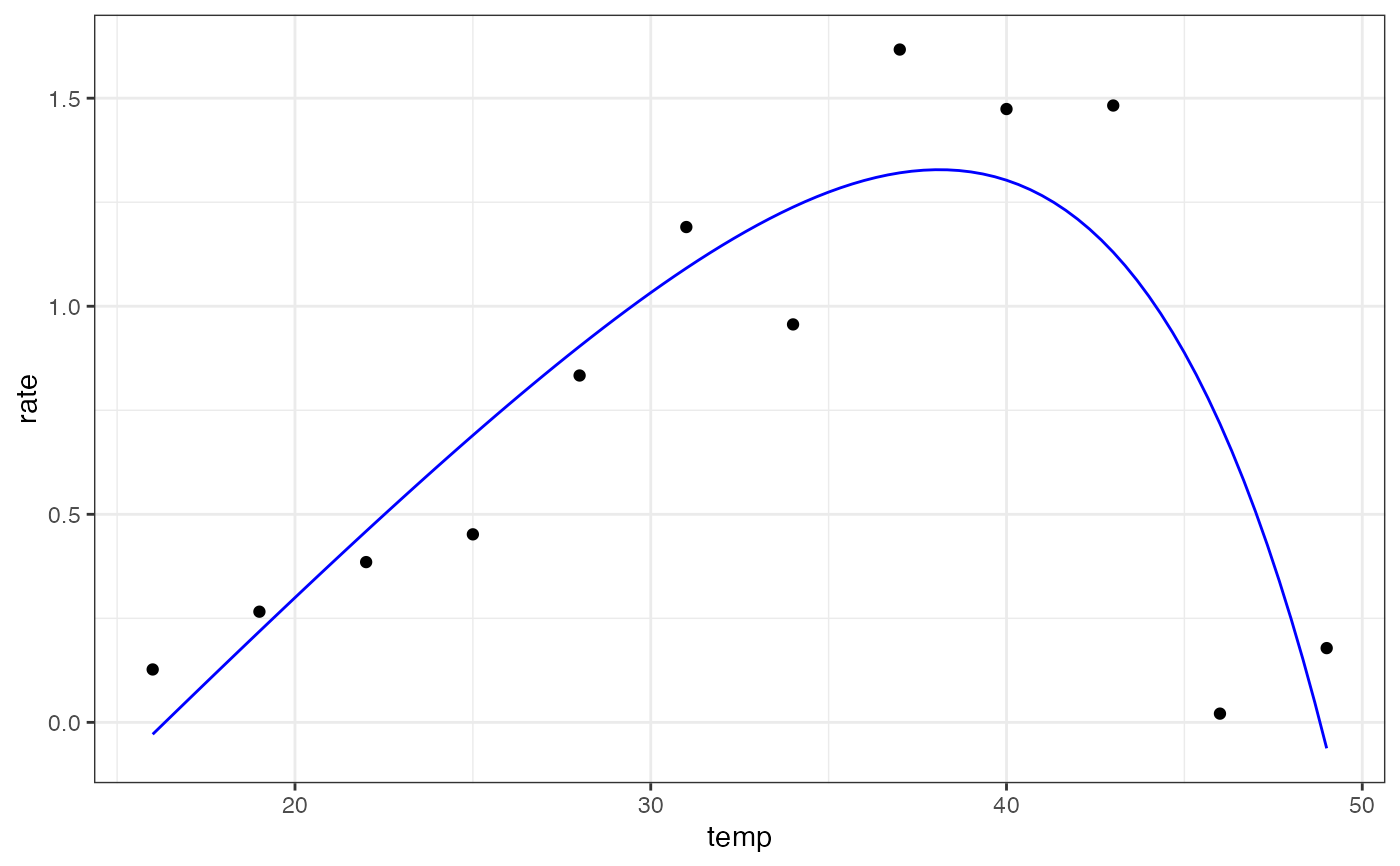
# plot
ggplot(preds) +
geom_point(aes(temp, rate), d) +
geom_line(aes(temp, .fitted), col = 'blue') +
theme_bw()