Pawar model for fitting thermal performance curves
Arguments
- temp
temperature in degrees centigrade
- r_tref
rate at the standardised temperature, tref
- e
activation energy (eV)
- eh
high temperature de-activation energy (eV)
- topt
optimum temperature (ºC)
- tref
standardisation temperature in degrees centigrade. Temperature at which rates are not inactivated by high temperatures
Value
a numeric vector of rate values based on the temperatures and parameter values provided to the function
Details
This model is a modified version of sharpeschoolhigh_1981 that explicitly models the optimum temperature.
Equation:
$$rate= \frac{r_{tref} \cdot exp^{\frac{-e}{k} (\frac{1}{temp + 273.15}-\frac{1}{t_{ref} + 273.15})}}{1 + (\frac{e}{eh - e}) \cdot exp^{\frac{e_h}{k}(\frac{1}{t_opt + 273.15}-\frac{1}{temp + 273.15})}}$$
where k is Boltzmann's constant with a value of 8.62e-05.
Start values in get_start_vals are derived from the data.
Limits in get_lower_lims and get_upper_lims are derived from the data or based extreme values that are unlikely to occur in ecological settings.
References
Kontopoulos, Dimitrios - Georgios, Bernardo García-Carreras, Sofía Sal, Thomas P. Smith, and Samraat Pawar. Use and Misuse of Temperature Normalisation in Meta-Analyses of Thermal Responses of Biological Traits. PeerJ. 6 (2018),
Examples
# load in ggplot
library(ggplot2)
library(nls.multstart)
# subset for the first TPC curve
data('chlorella_tpc')
d <- subset(chlorella_tpc, curve_id == 1)
# get start values and fit model
start_vals <- get_start_vals(d$temp, d$rate, model_name = 'pawar_2018')
# fit model
mod <- nls_multstart(rate~pawar_2018(temp = temp, r_tref, e, eh, topt, tref = 20),
data = d,
iter = c(3,3,3,3),
start_lower = start_vals - 10,
start_upper = start_vals + 10,
lower = get_lower_lims(d$temp, d$rate, model_name = 'pawar_2018'),
upper = get_upper_lims(d$temp, d$rate, model_name = 'pawar_2018'),
supp_errors = 'Y',
convergence_count = FALSE)
# look at model fit
summary(mod)
#>
#> Formula: rate ~ pawar_2018(temp = temp, r_tref, e, eh, topt, tref = 20)
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> r_tref 0.38722 0.08016 4.831 0.001303 **
#> e 0.58264 0.10186 5.720 0.000444 ***
#> eh 14.20311 12.83602 1.107 0.300668
#> topt 41.64610 0.77956 53.423 1.67e-11 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.1982 on 8 degrees of freedom
#>
#> Number of iterations to convergence: 21
#> Achieved convergence tolerance: 1.49e-08
#>
# get predictions
preds <- data.frame(temp = seq(min(d$temp), max(d$temp), length.out = 100))
preds <- broom::augment(mod, newdata = preds)
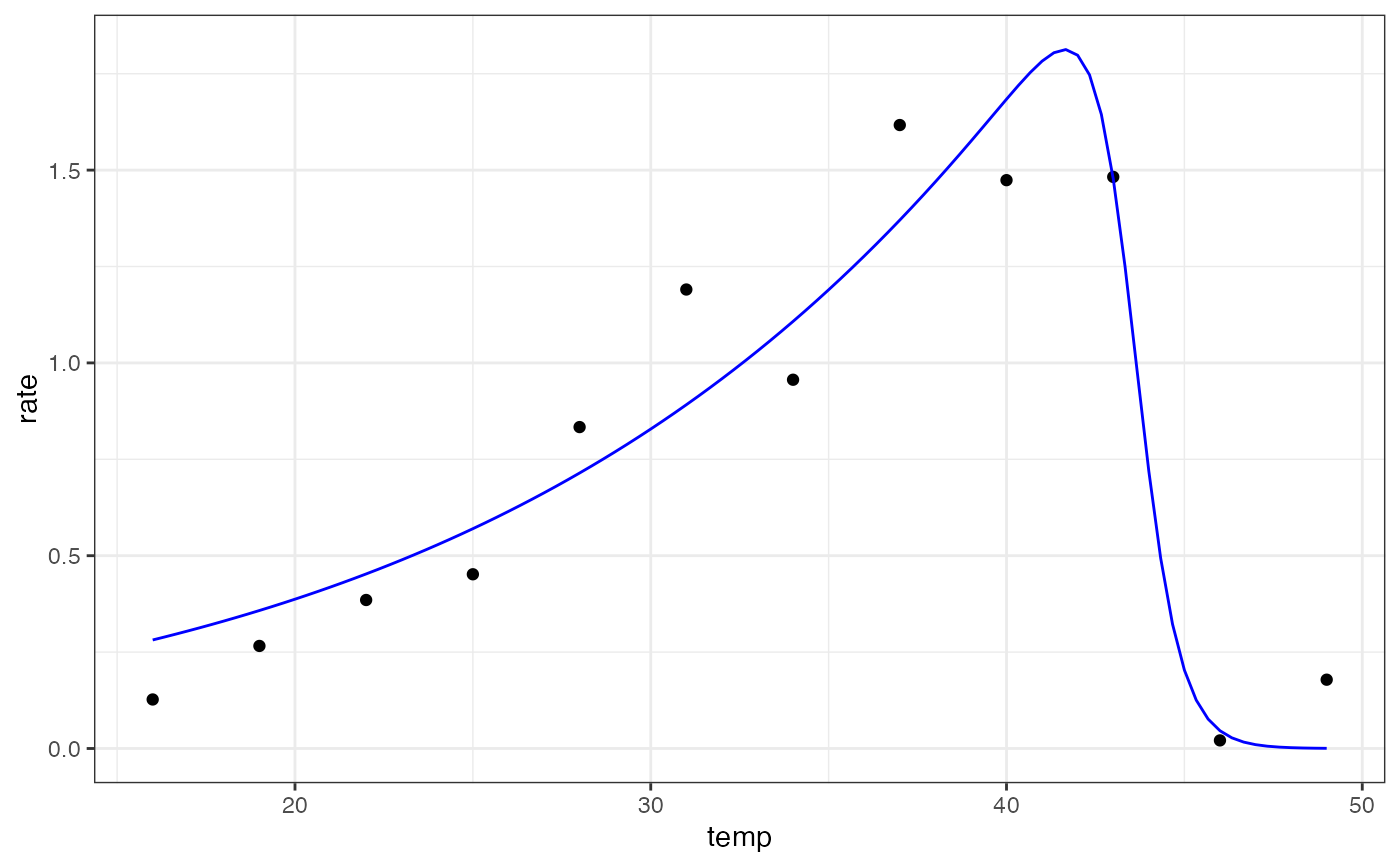
# plot
ggplot(preds) +
geom_point(aes(temp, rate), d) +
geom_line(aes(temp, .fitted), col = 'blue') +
theme_bw()